参考
一个完整的机器学习项目
主要步骤
- 项目概述
- 获取数据
- 发现并可视化数据,发现规律
- 为机器学习算法准备数据
- 选择模型,进行训练
- 微调模型
- 给出解决方案
- 部署、监控、维护系统
使用真实数据
- 流行的开源数据仓库
- 准入口(提供开源数据列表)
- 其他
项目概览
- 利用加州普查数据,建立一个加州房价模型。这个数据包含每个街区组的人口、收入中位数、房价中位数等指标。
划定问题
提出问题
- 第一个问题:商业目标是什么?如何使用、并从模型受益?
- 第二个问题:现在的解决方案效果如何?
划定问题
- 监督或非监督或强化学习?
- 分类或回归或其他?
- 批量还是线上?
选择性能指标
- 回归问题的典型指标:均方根误差(RMSE)、平方绝对误差(MAE)
核实假设
获取数据
下载数据
import os
import tarfile
from six.moves import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH = "datasets/housing"
HOUSING_URL = DOWNLOAD_ROOT + HOUSING_PATH + "/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
if not os.path.isdir(housing_path):
os.makedirs(housing_path)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
# fetch_housing_data()
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()
|
longitude |
latitude |
housing_median_age |
total_rooms |
total_bedrooms |
population |
households |
median_income |
median_house_value |
ocean_proximity |
| 0 |
-122.23 |
37.88 |
41.0 |
880.0 |
129.0 |
322.0 |
126.0 |
8.3252 |
452600.0 |
NEAR BAY |
| 1 |
-122.22 |
37.86 |
21.0 |
7099.0 |
1106.0 |
2401.0 |
1138.0 |
8.3014 |
358500.0 |
NEAR BAY |
| 2 |
-122.24 |
37.85 |
52.0 |
1467.0 |
190.0 |
496.0 |
177.0 |
7.2574 |
352100.0 |
NEAR BAY |
| 3 |
-122.25 |
37.85 |
52.0 |
1274.0 |
235.0 |
558.0 |
219.0 |
5.6431 |
341300.0 |
NEAR BAY |
| 4 |
-122.25 |
37.85 |
52.0 |
1627.0 |
280.0 |
565.0 |
259.0 |
3.8462 |
342200.0 |
NEAR BAY |
housing.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 20640 non-null float64
1 latitude 20640 non-null float64
2 housing_median_age 20640 non-null float64
3 total_rooms 20640 non-null float64
4 total_bedrooms 20433 non-null float64
5 population 20640 non-null float64
6 households 20640 non-null float64
7 median_income 20640 non-null float64
8 median_house_value 20640 non-null float64
9 ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
housing['ocean_proximity'].value_counts()
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64
housing.describe()
|
longitude |
latitude |
housing_median_age |
total_rooms |
total_bedrooms |
population |
households |
median_income |
median_house_value |
| count |
20640.000000 |
20640.000000 |
20640.000000 |
20640.000000 |
20433.000000 |
20640.000000 |
20640.000000 |
20640.000000 |
20640.000000 |
| mean |
-119.569704 |
35.631861 |
28.639486 |
2635.763081 |
537.870553 |
1425.476744 |
499.539680 |
3.870671 |
206855.816909 |
| std |
2.003532 |
2.135952 |
12.585558 |
2181.615252 |
421.385070 |
1132.462122 |
382.329753 |
1.899822 |
115395.615874 |
| min |
-124.350000 |
32.540000 |
1.000000 |
2.000000 |
1.000000 |
3.000000 |
1.000000 |
0.499900 |
14999.000000 |
| 25% |
-121.800000 |
33.930000 |
18.000000 |
1447.750000 |
296.000000 |
787.000000 |
280.000000 |
2.563400 |
119600.000000 |
| 50% |
-118.490000 |
34.260000 |
29.000000 |
2127.000000 |
435.000000 |
1166.000000 |
409.000000 |
3.534800 |
179700.000000 |
| 75% |
-118.010000 |
37.710000 |
37.000000 |
3148.000000 |
647.000000 |
1725.000000 |
605.000000 |
4.743250 |
264725.000000 |
| max |
-114.310000 |
41.950000 |
52.000000 |
39320.000000 |
6445.000000 |
35682.000000 |
6082.000000 |
15.000100 |
500001.000000 |
%matplotlib inline
import matplotlib.pyplot as plt
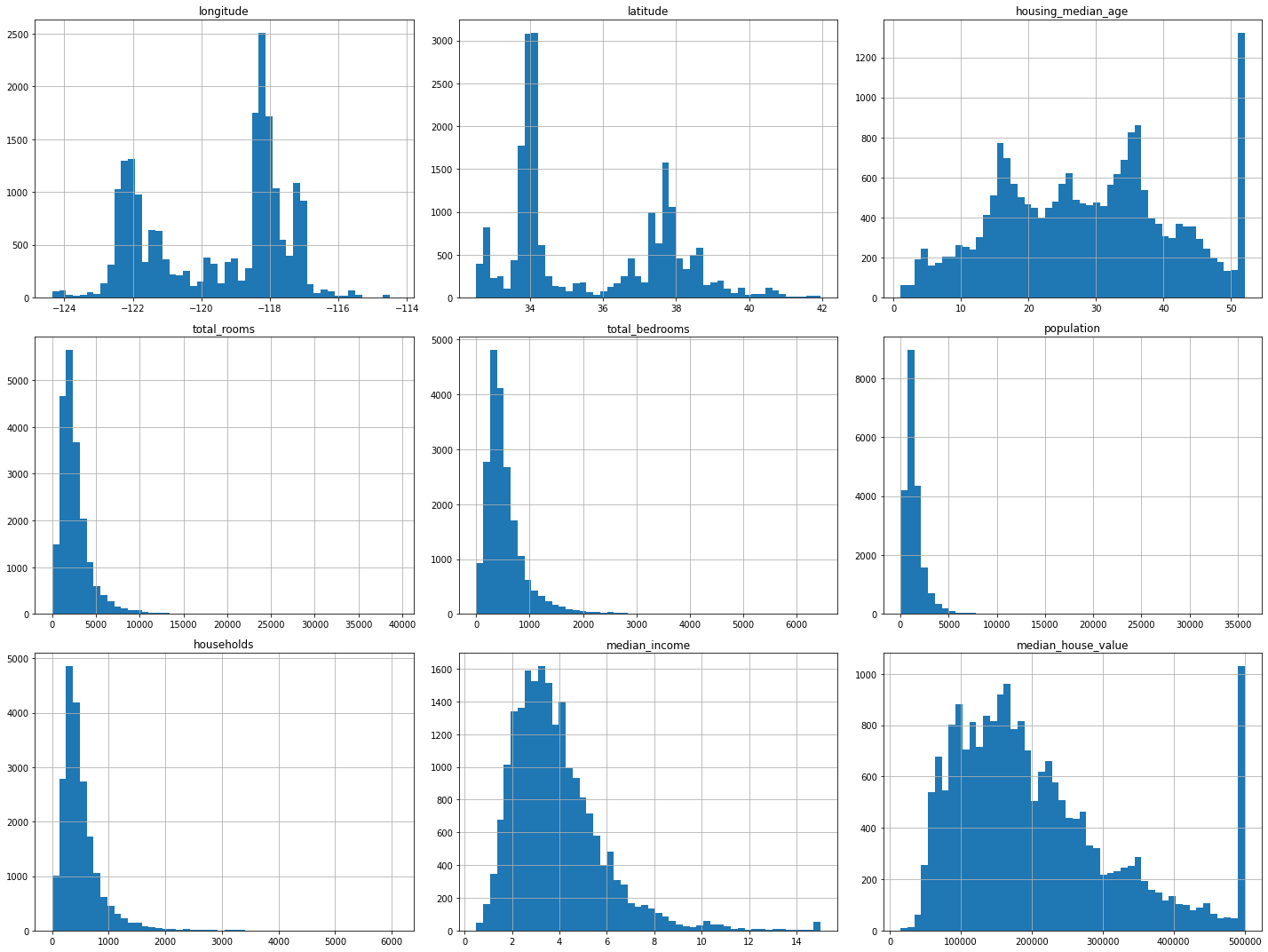
housing.hist(bins=50, figsize=(20, 15))
plt.tight_layout()
plt.show()
创建测试集
随机采样
import numpy as np
def train_test_split(data, test_ratio):
np.random.seed(0) # 设置随机数种子以每次运行产生相同测试集,但是新数据加入就可能把之前训练集的加入到测试集
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data)*test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = train_test_split(housing, test_ratio=0.2)
print(len(train_set), "train + ", len(test_set), "test")
16512 train + 4128 test
- 上述随机抽样如果新数据来,重新运行程序会将之前的训练样本有可能划分成测试样本
- 解决办法:一个通常的解决办法是使用每个实例的ID来判定这个实例是否应该放入测试集(假设每个实例都有唯一并且不变的ID)【例如,你可以计算出每个实例ID的哈希值,只保留其最后一个字节,如果该值小于等于51(约为256 的20%),就将其放入测试集。这样可以保证在多次运行中,测试集保持不变,即使更新了数据集。新的测试集会包含新实例中的20%,但不会有之前位于训练集的实例。】
import hashlib
def test_set_check(identifier, test_ratio, hash):
return hash(np.int64(identifier)).digest()[-1]<256*test_ratio
def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
return data.loc[~in_test_set], data.loc[in_test_set]
# 如果使用行索引作为唯一识别码,你需要保证新数据都放到现有数据的尾部,且没有行被删除
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
print(len(train_set), "train + ", len(test_set), "test")
16362 train + 4278 test
# 一个区的维度和经度在几百万年之内是不变的,所以可以将两者结合成一个ID
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id")
print(len(train_set), "train + ", len(test_set), "test")
16267 train + 4373 test
# 最简单的函数是train_test_split ,它的作用和之前的函数split_train_test 很像,并带有其它一些功能。首先,它有一个random_state 参数,可以设定前面讲过的随机生成器种子;第二,你可以将种子传递给多个行数相同的数据集,可以在相同的索引上分割数据集(这个功能非常有用,比如你的标签值是放在另一个DataFrame 里的)
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
print(len(train_set), "train + ", len(test_set), "test")
16512 train + 4128 test
- 目前为止,我们采用的都是纯随机的取样方法。当你的数据集很大时(尤其是和属性数相比),这通常可行;但如果数据集不大,就会有采样偏差的风险。
分层采样
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"]<5, 5.0, inplace=True)
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
print(len(strat_train_set), "train + ", len(strat_test_set), "test")
16512 train + 4128 test
housing["income_cat"].value_counts() / len(housing)
3.0 0.350581
2.0 0.318847
4.0 0.176308
5.0 0.114438
1.0 0.039826
Name: income_cat, dtype: float64
strat_train_set["income_cat"].value_counts() / len(strat_train_set)
3.0 0.350594
2.0 0.318859
4.0 0.176296
5.0 0.114402
1.0 0.039850
Name: income_cat, dtype: float64
for set in (strat_train_set, strat_test_set):
set.drop(["income_cat"], axis=1, inplace=True)
数据EDA
- 首先将测试集放一旁,只研究训练集
- 如果训练集非常大,需要再采样一个探索集
housing = strat_train_set.copy()
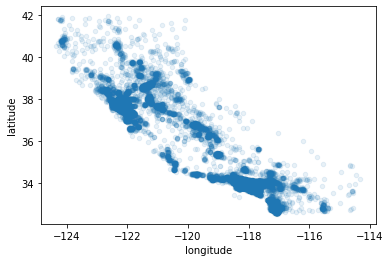
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1) # alpha控制透明度
<AxesSubplot:xlabel='longitude', ylabel='latitude'>
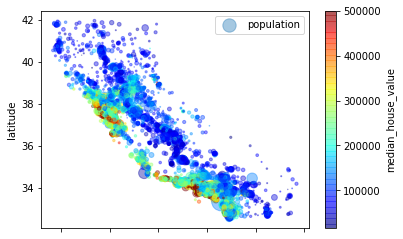
housing.plot(kind='scatter', x="longitude", y="latitude", alpha=0.4,
s=housing['population']/100, label='population',
c='median_house_value', cmap=plt.get_cmap('jet'), colorbar=True)
plt.legend()
<matplotlib.legend.Legend at 0x1cb9a343b50>
查找关联
# 相关系数
corr_matrix = housing.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)
median_house_value 1.000000
median_income 0.687160
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population -0.026920
longitude -0.047432
latitude -0.142724
Name: median_house_value, dtype: float64
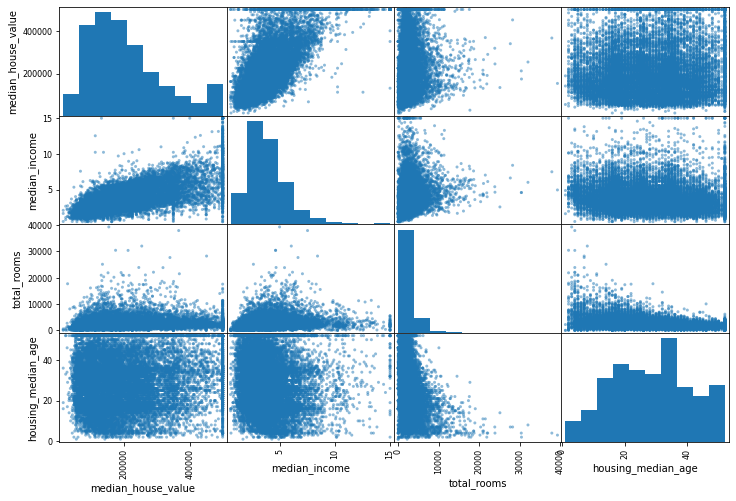
# 相关系数图
from pandas.plotting import scatter_matrix
attributes = ['median_house_value', 'median_income', 'total_rooms', 'housing_median_age']
scatter_matrix(housing[attributes], figsize=(12,8))
array([[<AxesSubplot:xlabel='median_house_value', ylabel='median_house_value'>,
<AxesSubplot:xlabel='median_income', ylabel='median_house_value'>,
<AxesSubplot:xlabel='total_rooms', ylabel='median_house_value'>,
<AxesSubplot:xlabel='housing_median_age', ylabel='median_house_value'>],
[<AxesSubplot:xlabel='median_house_value', ylabel='median_income'>,
<AxesSubplot:xlabel='median_income', ylabel='median_income'>,
<AxesSubplot:xlabel='total_rooms', ylabel='median_income'>,
<AxesSubplot:xlabel='housing_median_age', ylabel='median_income'>],
[<AxesSubplot:xlabel='median_house_value', ylabel='total_rooms'>,
<AxesSubplot:xlabel='median_income', ylabel='total_rooms'>,
<AxesSubplot:xlabel='total_rooms', ylabel='total_rooms'>,
<AxesSubplot:xlabel='housing_median_age', ylabel='total_rooms'>],
[<AxesSubplot:xlabel='median_house_value', ylabel='housing_median_age'>,
<AxesSubplot:xlabel='median_income', ylabel='housing_median_age'>,
<AxesSubplot:xlabel='total_rooms', ylabel='housing_median_age'>,
<AxesSubplot:xlabel='housing_median_age', ylabel='housing_median_age'>]],
dtype=object)
# 最有希望用来预测房价中位数的属性是收入中位数,因此将这张图放大
housing.plot(kind='scatter', x='median_income', y='median_house_value', alpha=0.1)
<AxesSubplot:xlabel='median_income', ylabel='median_house_value'>
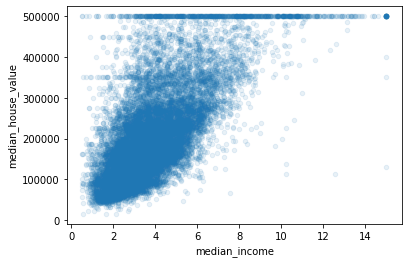
- 会发现一些直线,希望去除这些直线对应的记录,以防止算法重复这些巧合
属性组合试验
- 探索数据可能发现一些数据的巧合,需要将其去除
- 发现一些属性间有趣的关联
- 一些属性有长尾分布,将其转换
- ……
housing['rooms_per_household'] = housing['total_rooms'] / housing['households']
housing['bedrooms_per_room'] = housing['total_bedrooms'] / housing['total_rooms']
housing['population_per_household'] = housing['population'] / housing['households']
corr_matrix = housing.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)
median_house_value 1.000000
median_income 0.687160
rooms_per_household 0.146285
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population_per_household -0.021985
population -0.026920
longitude -0.047432
latitude -0.142724
bedrooms_per_room -0.259984
Name: median_house_value, dtype: float64
为机器学习算法准备数据
- 写函数的好处:
- 函数可以让你在任何数据集上方便的进行重复数据转换
- 你能慢慢建立一个转换函数库,可以在未来的项目中复用
- 在将数据传给算法之前,你可以在实时系统中使用这些函数
- 这可以让你方便的尝试多种数据转换,查看哪些转换方法结合起来效果最好
housing = strat_train_set.drop('median_house_value', axis=1)
housing_labels = strat_train_set['median_house_value'].copy()
数据清洗
- 前面探索发现
total_bedrooms有一些缺失值,有三个解决选项:
- 去掉对应行记录
- 去掉这个属性
- 进行赋值(0、平均值、中位数等等)
- 也可以使用sklearn里面的Imputer类来处理缺失值
housing.dropna(subset=['total_bedrooms']) # 选项1
housing.drop('total_bedrooms', axis=1) # 选项2
median = housing['total_bedrooms'].median() # 选项3
housing['total_bedrooms'].fillna(median)
17606 351.0
18632 108.0
14650 471.0
3230 371.0
3555 1525.0
...
6563 236.0
12053 294.0
13908 872.0
11159 380.0
15775 682.0
Name: total_bedrooms, Length: 16512, dtype: float64
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(missing_values=np.nan, strategy='median')
# 只有数值属性才能算出中位数
housing_num = housing.drop('ocean_proximity', axis=1)
imputer.fit(housing_num)
print(imputer.statistics_)
print(housing.median().values)
# 对训练集进行转换
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns)
housing_tr.head()
[-118.51 34.26 29. 2119.5 433. 1164. 408.
3.5409]
[-118.51 34.26 29. 2119.5 433. 1164. 408.
3.5409]
|
longitude |
latitude |
housing_median_age |
total_rooms |
total_bedrooms |
population |
households |
median_income |
| 0 |
-121.89 |
37.29 |
38.0 |
1568.0 |
351.0 |
710.0 |
339.0 |
2.7042 |
| 1 |
-121.93 |
37.05 |
14.0 |
679.0 |
108.0 |
306.0 |
113.0 |
6.4214 |
| 2 |
-117.20 |
32.77 |
31.0 |
1952.0 |
471.0 |
936.0 |
462.0 |
2.8621 |
| 3 |
-119.61 |
36.31 |
25.0 |
1847.0 |
371.0 |
1460.0 |
353.0 |
1.8839 |
| 4 |
-118.59 |
34.23 |
17.0 |
6592.0 |
1525.0 |
4459.0 |
1463.0 |
3.0347 |
处理文本和类别属性
- 将文本标签转换为数字:这样做的问题是:ML算法会认为两个临近值比两个疏远值更相似,但是对标签数据这样是不准确的
- sklearn提供一个转换器:LabelEncoder
- one-hot编码:每个属性弄成0-1
- sklearn提供一个转换器:OneHotEncoder
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
housing_cat = housing['ocean_proximity']
housing_cat_encoded = encoder.fit_transform(housing_cat)
print(housing_cat_encoded)
# 有多个文本特征列时,应使用factorize()方法
housing_cat_encoded, housing_categories = housing_cat.factorize()
print(housing_cat_encoded, housing_categories)
print(encoder.classes_)
[0 0 4 ... 1 0 3]
[0 0 1 ... 2 0 3] Index(['<1H OCEAN', 'NEAR OCEAN', 'INLAND', 'NEAR BAY', 'ISLAND'], dtype='object')
['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN']
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
housing_cat_1hot = encoder.fit_transform(housing_cat_encoded.reshape(-1,1))
print(housing_cat_1hot.toarray())
housing_cat_1hot # 稀疏矩阵
[[1. 0. 0. 0. 0.]
[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
...
[0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]]
<16512x5 sparse matrix of type '<class 'numpy.float64'>'
with 16512 stored elements in Compressed Sparse Row format>
# 使用LabelBinarize一步到位:获得稀疏矩阵+to array
from sklearn.preprocessing import LabelBinarizer
encoder = LabelBinarizer(sparse_output=False)
housing_cat_1hot = encoder.fit_transform(housing_cat)
print(housing_cat_1hot)
# # 有多个文本特征列时,应使用sklearn中的CategoricalEncoder类
# from sklearn.preprocessing import CategoricalEncoder
[[1 0 0 0 0]
[1 0 0 0 0]
[0 0 0 0 1]
...
[0 1 0 0 0]
[1 0 0 0 0]
[0 0 0 1 0]]
自定义转换器
- 尽管Scikit-Learn 提供了许多有用的转换器,你还是需要自己动手写转换器执行任务,比如自定义的清理操作,或属性组合。你需要让自制的转换器与Scikit-Learn 组件(比如流水线)无缝衔接工作,因为Scikit-Learn 是依赖鸭子类型的(而不是继承),你所需要做的是创建一个类并执行三个方法:fit() (返回self ),transform() ,和fit_transform() 。
- 鸭子类型(英语:duck typing)在程序设计中是动态类型的一种风格。在这种风格中,一个对象有效的语义,不是由继承自特定的类或实现特定的接口,而是由”当前方法和属性的集合”决定。
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, household_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_pre_room=True):
self.add_bedrooms_pre_room = add_bedrooms_pre_room
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
rooms_pre_household = X[:, rooms_ix] / X[:, household_ix]
population_pre_household = X[:, population_ix] / X[:, household_ix]
if self.add_bedrooms_pre_room:
bedrooms_pre_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_pre_household, population_pre_household, bedrooms_pre_room]
else:
return np.c_[X, rooms_pre_household, population_pre_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_pre_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)
housing_extra_attribs
array([[-121.89, 37.29, 38.0, ..., '<1H OCEAN', 4.625368731563422,
2.094395280235988],
[-121.93, 37.05, 14.0, ..., '<1H OCEAN', 6.008849557522124,
2.7079646017699117],
[-117.2, 32.77, 31.0, ..., 'NEAR OCEAN', 4.225108225108225,
2.0259740259740258],
...,
[-116.4, 34.09, 9.0, ..., 'INLAND', 6.34640522875817,
2.742483660130719],
[-118.01, 33.82, 31.0, ..., '<1H OCEAN', 5.50561797752809,
3.808988764044944],
[-122.45, 37.77, 52.0, ..., 'NEAR BAY', 4.843505477308295,
1.9859154929577465]], dtype=object)
特征缩放
- 让所有属性具有相同量度:
- 线性归一化: MinMaxScaler()
- 标准化: StandarScaler()
- 与所有的转换一样,缩放器只能向训练集拟合,而不是向完整的数据集(包括测试集)。只有这样,你才能用缩放器转换训练集和测试集(和新数据)
转换流水线
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipline = Pipeline([('imputer', SimpleImputer(strategy='median')),
('attribs_addr', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
housing_num_tr = num_pipline.fit_transform(housing_num)
housing_num_tr
array([[-1.15604281, 0.77194962, 0.74333089, ..., -0.31205452,
-0.08649871, 0.15531753],
[-1.17602483, 0.6596948 , -1.1653172 , ..., 0.21768338,
-0.03353391, -0.83628902],
[ 1.18684903, -1.34218285, 0.18664186, ..., -0.46531516,
-0.09240499, 0.4222004 ],
...,
[ 1.58648943, -0.72478134, -1.56295222, ..., 0.3469342 ,
-0.03055414, -0.52177644],
[ 0.78221312, -0.85106801, 0.18664186, ..., 0.02499488,
0.06150916, -0.30340741],
[-1.43579109, 0.99645926, 1.85670895, ..., -0.22852947,
-0.09586294, 0.10180567]])
将数值流水线和属性型流水线一起处理
from sklearn.pipeline import FeatureUnion
from sklearn.base import BaseEstimator, TransformerMixin
class DataFrameSelector(BaseEstimator, TransformerMixin):
def __init__(self, attribute_names):
self.attribute_names=attribute_names
def fit(self, X, y=None):
return self
def transform(self, X):
return X[self.attribute_names].values
class MyLabelBinarizer(BaseEstimator, TransformerMixin):
def __init__(self, *args, **kwargs):
self.encoder = LabelBinarizer(*args, **kwargs)
def fit(self, x, y=None):
self.encoder.fit(x)
return self
def transform(self, x, y=None):
return self.encoder.transform(x)
num_attribs = list(housing_num)
cat_attribs = ['ocean_proximity']
num_pipline = Pipeline([('selector', DataFrameSelector(num_attribs)),
('imputer', SimpleImputer(strategy='median')),
('attribs_addr', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
cat_pipline = Pipeline([('selector', DataFrameSelector(cat_attribs)),
('label_binarizer', MyLabelBinarizer()),
])
full_pipeline = FeatureUnion(transformer_list=[('num_pipeline', num_pipline),
('cat_pipeline', cat_pipline),
])
housing_prepared = full_pipeline.fit_transform(housing)
housing_prepared.shape
(16512, 16)
选择并训练模型
- 前面已做
- 限定了问题
- 获取数据
- 探索数据
- 采样测试集
- 自动化的转换流水线:清理数据
在训练集上训练和评估
# 回归模型
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression();
lin_reg.fit(housing_prepared, housing_labels);
# 用一些训练数据看看
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print(lin_reg.predict(some_data_prepared))
print(list(some_labels))
[210644.60459286 317768.80697211 210956.43331178 59218.98886849
189747.55849879]
[286600.0, 340600.0, 196900.0, 46300.0, 254500.0]
# 计算RSME
from sklearn.metrics import mean_squared_error
housing_pred = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_pred)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
68628.19819848923
- 显然回归模型欠拟合,特征没有提供足够多的信息来做一个好的预测,或者模型不够强大
# 决策树
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor();
tree_reg.fit(housing_prepared, housing_labels);
housing_pred = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_pred)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
0.0
使用交叉验证来做更佳的评估
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring='neg_mean_squared_error', cv=10)
tree_rmse_scores = np.sqrt(-scores)
tree_rmse_scores
array([70402.31297471, 67320.10682085, 70223.47037104, 69614.92234167,
71787.54609682, 75496.45097963, 71048.37280966, 71597.08425246,
77043.79328191, 70578.37265691])
def displayScores(scores):
print("Scores:", scores)
print("Mean:", scores.mean())
print("Std:", scores.std())
displayScores(tree_rmse_scores)
Scores: [70402.31297471 67320.10682085 70223.47037104 69614.92234167
71787.54609682 75496.45097963 71048.37280966 71597.08425246
77043.79328191 70578.37265691]
Mean: 71511.24325856709
Std: 2677.852533862523
scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring='neg_mean_squared_error', cv=10)
lin_rmse_scores = np.sqrt(-scores)
lin_rmse_scores
array([66782.73843989, 66960.118071 , 70347.95244419, 74739.57052552,
68031.13388938, 71193.84183426, 64969.63056405, 68281.61137997,
71552.91566558, 67665.10082067])
displayScores(lin_rmse_scores)
Scores: [66782.73843989 66960.118071 70347.95244419 74739.57052552
68031.13388938 71193.84183426 64969.63056405 68281.61137997
71552.91566558 67665.10082067]
Mean: 69052.46136345083
Std: 2731.6740017983425
- 判断没错:决策树模型过拟合很严重,它的性能比线性回归模型还差
# 随机森林
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
housing_pred = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_pred)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
18691.633224101523
scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
scoring='neg_mean_squared_error', cv=10)
forest_rmse_scores = np.sqrt(-scores)
forest_rmse_scores
array([49503.09765569, 47556.24185705, 49876.34879458, 52163.99071947,
49535.73021436, 53483.37725634, 48882.69703437, 47583.62724759,
53339.88235391, 49722.75212307])
displayScores(forest_rmse_scores)
Scores: [49503.09765569 47556.24185705 49876.34879458 52163.99071947
49535.73021436 53483.37725634 48882.69703437 47583.62724759
53339.88235391 49722.75212307]
Mean: 50164.77452564256
Std: 2032.5814147343965
- 在继续深入前,应该尝试下不同模型,不要在调节超参数上花费太多时间,目标是列出一个可能的模型列表(2-5个)
# 保存模型
import joblib
output_path = 'model/'
if not os.path.isdir(output_path):
os.makedirs(output_path)
joblib.dump(forest_reg, output_path+'forest_reg.pkl');
import gc
del forest_reg
gc.collect();
forest_reg = joblib.load(output_path + 'forest_reg.pkl')
forest_reg.predict(housing_prepared)
array([267951. , 323307. , 221516. , ..., 102155. , 214044. ,
464662.73])
模型微调
- 假设有一个列表了,列表里面有几个有希望的模型了,现在对它们进行微调
- 网格搜索
- 随即搜索
- 集成方法
网格搜索
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators': [3,10,30], 'max_features': [2,4,6,8]},
{'bootstrap': [False], 'n_estimators': [3,10], 'max_features': [2,3,4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared, housing_labels)
(grid_search.best_params_)
(grid_search.best_estimator_)
RandomForestRegressor(max_features=6, n_estimators=30)
- param_grid 告诉Scikit-Learn 首先评估所有的列在第一个dict 中的n_estimators 和max_features 的3 × 4 = 12 种组合(不用担心这些超参数的含义,会在第7 章中解释)。然后尝试第二个dict 中超参数的2 × 3 = 6 种组合,这次会将超参数bootstrap 设为False 而不是True (后者是该超参数的默认值)。
- 总之,网格搜索会探索12 + 6 = 18 种RandomForestRegressor 的超参数组合,会训练每个模型五次(因为用的是五折交叉验证)。换句话说,训练总共有18 × 5 = 90 轮!K 折将要花费大量时间,完成后,你就能获得参数的最佳组合
# 评估评分
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres['mean_test_score'], cvres['params']):
print(np.sqrt(-mean_score), params)
64484.368945438095 {'max_features': 2, 'n_estimators': 3}
55801.68474277632 {'max_features': 2, 'n_estimators': 10}
53103.397117972374 {'max_features': 2, 'n_estimators': 30}
60739.34011042108 {'max_features': 4, 'n_estimators': 3}
52606.55731138118 {'max_features': 4, 'n_estimators': 10}
50461.78456229793 {'max_features': 4, 'n_estimators': 30}
58694.1806275357 {'max_features': 6, 'n_estimators': 3}
52167.01603965681 {'max_features': 6, 'n_estimators': 10}
49789.76142728186 {'max_features': 6, 'n_estimators': 30}
59244.45170151536 {'max_features': 8, 'n_estimators': 3}
52471.88272318626 {'max_features': 8, 'n_estimators': 10}
50024.71009745971 {'max_features': 8, 'n_estimators': 30}
62288.45521151971 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3}
54541.851530599495 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10}
60763.31894922859 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3}
52256.3308785951 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10}
58006.11393494447 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
51525.95227740632 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}
随机搜索
- 当超参数的搜索空间很大时,最好使用
RandomizedSearchCV
- 随机搜索通过选择每个超参数的一个随机值的特定数量的随机组合,两个优点:
- 如果你让随机搜索运行,比如1000 次,它会探索每个超参数的1000 个不同的值(而不是像网格搜索那样,只搜索每个超参数的几个值
- 你可以方便地通过设定搜索次数,控制超参数搜索的计算量
from sklearn.model_selection import RandomizedSearchCV
distributions = dict(n_estimators=[3,10,30], max_features=[2,4,6,8])
forest_reg = RandomForestRegressor()
grid_search = RandomizedSearchCV(forest_reg, distributions,
random_state=0, cv=5,
scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared, housing_labels)
(grid_search.best_params_)
(grid_search.best_estimator_)
RandomForestRegressor(max_features=8, n_estimators=30)
# 评估评分
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres['mean_test_score'], cvres['params']):
print(np.sqrt(-mean_score), params)
60313.361125661046 {'n_estimators': 3, 'max_features': 6}
49834.72365719627 {'n_estimators': 30, 'max_features': 8}
52515.52121503662 {'n_estimators': 10, 'max_features': 4}
51547.81101848066 {'n_estimators': 10, 'max_features': 8}
52824.54605534015 {'n_estimators': 30, 'max_features': 2}
50011.013090069086 {'n_estimators': 30, 'max_features': 6}
55772.624674081875 {'n_estimators': 10, 'max_features': 2}
51994.5987814074 {'n_estimators': 10, 'max_features': 6}
58695.313520315474 {'n_estimators': 3, 'max_features': 8}
60144.83595308729 {'n_estimators': 3, 'max_features': 4}
集成方法
- 另一种微调系统的方法是将表现最好的模型组合起来。组合(集成)之后的性能通常要比单独的模型要好(就像随机森林要比单独的决策树要好),特别是当单独模型的误差类型不同时
分析最佳模型和它们的误差
- 根据特征重要性,丢弃一些无用特征
- 观察系统误差,搞清为什么有这些误差,如何改正问题(添加、去掉、清洗异常值等措施)
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances
array([6.54145890e-02, 6.11239658e-02, 4.68569762e-02, 1.57799553e-02,
1.47877860e-02, 1.52606278e-02, 1.45150045e-02, 3.56582379e-01,
5.46405542e-02, 1.14200534e-01, 7.60282167e-02, 7.53161308e-03,
1.52163827e-01, 3.13174862e-05, 2.25971757e-03, 2.82293596e-03])
extra_attribs = ['rooms_per_hold', 'pop_per_hold', 'bedrooms_per_room']
cat_ont_hot_attribs = list(encoder.classes_)
attributes = num_attribs + extra_attribs + cat_ont_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)
[(0.35658237869153536, 'median_income'),
(0.1521638272583547, 'INLAND'),
(0.11420053447156554, 'pop_per_hold'),
(0.07602821669031448, 'bedrooms_per_room'),
(0.06541458900157228, 'longitude'),
(0.06112396584108679, 'latitude'),
(0.05464055415192507, 'rooms_per_hold'),
(0.04685697616305872, 'housing_median_age'),
(0.015779955349765996, 'total_rooms'),
(0.015260627821204058, 'population'),
(0.01478778596813993, 'total_bedrooms'),
(0.014515004497103572, 'households'),
(0.007531613076317472, '<1H OCEAN'),
(0.0028229359597008235, 'NEAR OCEAN'),
(0.0022597175721814156, 'NEAR BAY'),
(3.131748617381553e-05, 'ISLAND')]
用测试集评估系统
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop('median_house_value', axis=1)
y_test = strat_test_set['median_house_value'].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse
48237.045259350096
项目预上线阶段
- 展示方案
- 学到了什么
- 做了什么
- 没做什么
- 做过什么假设
- 系统的限制是什么
- ……
启动、监控、维护系统
- 接入输入数据,编写测试
- 编写监控代码
- 编写评估系统
实践!








