基础
问题
- 如何给众多网页排名?
解决
- 一个解决办法:
- 当很多网页都链接到同一个网页时,那这个网页应该排名靠前
- 链接这个网页的众多网页中,排名越靠前的网页,其重要性应该更高
PageRank
- $PR_i$表示第$i$个网页的
PageRank值,代表其网页排名依据 - $V$是所有网页集合
- $O_j$是第$j$个网页所存在的外链数,越多外链,它给$i$网页投票对应重要性越低
使用图构建PageRank
网页对应图的节点
node网页$i$的外链有网页$j$代表$(i,j)$,即图的有向边
edge如下图所示:
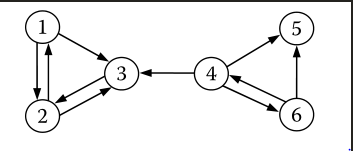
表示为$G(V,E)$,上图的邻接矩阵表示为:
用矩阵表示
式(1):$P=A^TP$其中$P=[PR_1, PR_2, …, PR_n]^T$
如何求解
先给每个网页给定一个初始$PR$值,一般都是$1/n$
然后使用$P=A^TP$进行迭代,直到$||P^k - P^{k-1}||< \epsilon$,这是一个马尔可夫收敛过程
但是需要邻接矩阵$A$满足下面3个条件上式才有解:
- 转移概率矩阵
(stochastic matrix):即每行至少有一个非零值 - 不可约性:矩阵A对应的有向图必须是强连通的,即任意两个节点,存在一条路径可达
- 非周期性:即存在一个最小正整数$k$,使得从某节点$i$出发又回到状态$i$的所有路径长度是$k$的整数倍,这就需要阻尼系数
d
- 转移概率矩阵
一般情况下矩阵$A$不满足上述三个条件,故需要对求解式作平滑处理,最终等式如下:
其中:$d \in [0,1],I\text{是单位阵}$
最终求解式
优缺点
- 缺点:旧的页面的排名往往会比新页面高
- 因为即使是质量很高的新页面也往往不会有很多外链,除非它是某个已经存在站点的子站点。这也是
PageRank需要多项算法结合以保证其结果的准确性的原因
- 因为即使是质量很高的新页面也往往不会有很多外链,除非它是某个已经存在站点的子站点。这也是



