原理介绍
Title
Follow-the-Regularized-Leader and Mirror Descent: Equivalence Theorems and L1 Regularization
Abstract
【原文】
We prove that many mirror descent algorithms for online convex optimization (such as online gradient descent) have an equivalent interpretation as follow-the-regularizedleader (FTRL) algorithms. This observation makes the relationships between many commonly used algorithms explicit, and provides theoretical insight on previous experimental observations. In particular, even though the FOBOS composite mirror descent algorithm handles L1 regularization explicitly, it has been observed that the FTRL-style Regularized Dual Averaging (RDA) algorithm is even more e ective at producing sparsity. Our results demonstrate that the key di erence between these algorithms is how they handle the cumulative L1 penalty. While FOBOS handles the L1 term exactly on any given update, we show that it is e ectively using subgradient approximations to the L1 penalty from previous rounds, leading to less sparsity than RDA, which handles the cumulative penalty in closed form. The FTRL-Proximal algorithm, which we introduce, can be seen as a hybrid of these two algorithms, and signi cantly outperforms both on a large, realworld dataset.
【译文】
我们证明了许多用于在线凸优化的镜像下降算法(例如在线梯度下降)具有与follow-the-regularizedleader (FTRL)算法等效的解释。该观察使许多常用算法之间的关系变得明确,并提供了对先前实验观察的理论见解。尤其是,即使FOBOS复合镜像下降算法可以明确处理L1正则化,也已经观察到FTRL样式的正则平均化(RDA)算法在产生稀疏性方面更为有效。我们的结果表明,这些算法之间的关键区别在于它们如何处理累积的L1损失。尽管FOBOS可以在任何给定的更新中精确地处理L1项,但我们证明它有效地使用了前几轮对L1罚分的次梯度近似,导致稀疏性低于RDA,后者以封闭形式处理累积罚分。我们介绍的FTRL-Proximal算法可以看作是这两种算法的混合体,在大型的真实数据集上均远胜过两者。
1 Introduction
【原文】


【译文】
我们考虑了在线凸优化的问题及其在在线学习中的应用。 在每一轮中,$t=1,…,T$,我们选择一个点$x_t\in R^n$。 然后揭示了凸损失函数$f_t$以及损失$f_t(x_t)$。在这项工作中,我们研究了在线凸优化的两个最重要且成功的低regret算法家族之间的关系。 从表面上看,诸如Regularized Dual Averaging [Xiao,2009]之类的正规化领导算法与FOBOS [Duchi and Singer,2009]等梯度下降(更普遍的是镜像下降)风格的算法似乎有所不同。 但是,这里我们表明,在二次稳定正则化的情况下,算法之间基本上只有两个区别:
【原文】

【译文】
- 它们如何选择将额外的强凸性用于保证低regret:RDA将正则化集中在原点,而FOBOS将正则化集中在当前可行点。
- 它们如何处理任意的非光滑正则化函数。这包括投影到可行集的机制以及如何处理L1正则化。

【译文】
为了使这些区别更精确,同时也说明这些家族实际上是密切相关的,我们考虑第三种算法,FTRL-Proximal。当省略非光滑项时,该算法实际上与FOBOS是相同的。另一方面,其更新与对偶平均的更新基本相同,只是增加的强凸性以当前可行点为中心(见表1)。
【表1】

【原文】

【译文】
先前的工作已通过实验表明,采用L1正则化进行对偶平均比引入FOBOS更有效地引入稀疏性[Xiao,2009,Duchi et al.,2010a]。我们的等价定理对此提供了理论上的解释:RDA考虑了第t轮的累积L1惩罚$ t\lambda ||x||_1 $,FOBOS(当使用等价定理视为全局优化时)考虑$\phi_{1:t-1}*x+\lambda||x||_1$,其中$\phi_s$是确定的$\lambda||x_s||_1$的次梯度近似(我们用$\phi_{1:t-1}$代表$\sum_{s=1}^{t-1}{\phi_s}$,并根据需要将表示法扩展为矩阵和函数的和)。
【原文】


【译文】
在第2节中,我们考虑了镜像下降和遵循正则化领导的一般公式,并证明了与两者有关的定理。 在第3节中,我们将通过实验比较FOBOS,RDA和FTRL-Proximal。 FTRL-Proximal算法在稀疏性方面的行为与RDA非常相似,认为是L1罚则的累积次梯度近似导致FOBOS稀疏性降低。
近年来,在线梯度下降和随机梯度下降(其批次模拟)已证明自己是用于大规模机器学习的出色算法。 在最简单的情况下,FTLR-Proximal是相同的,但是当需要L1或其他不平滑的正则化时,FTRL-Proximal的性能明显优于FOBOS,并且也可以优于RDA。 由于FTRL-Proximal和RDA的实现仅需要几行代码,因此我们建议您尝试两者并在实践中选择性能最佳的代码。
算法
【原文】

【译文】
我们首先建立符号并更正式地介绍我们考虑的算法。 虽然我们的定理适用于这些算法的更通用版本,但在这里我们集中于我们在实验中使用的特定实例。我们考虑损失函数$f_t(x)=l_t(x)+\Phi(x)$,其中$\Phi(x)$(通常不平滑)是固定的正则化函数。在典型的在线学习环境中,给定一个样本$(\theta_t,y_t)$,$\theta_t \in R^n$是特征向量,$y_t \in \{-1,1\}$是label,我们得到$l_t(x)=loss(\theta_tx,y_t)$。例如,对逻辑回归来说用的是log-loss,$loss(\theta_tx,y_t)=log(1+\exp(-y_t\theta_tx))$。对线性函数我们使用标准规约法,令$g_t=\nabla{l_t(x_t)}$。我们考虑的所有算法都支持复合更新(显示考虑$\Phi$而不是通过梯度$\nabla{f_t(x_t)}$以及可自适应选择的正半定学习率矩阵Q(将这些矩阵解释为学习率将在第2节中有说明))
【原文】


【译文】
我们考虑的第一个算法是来自梯度下降家族的FOBOS,如下:
我们隐式地将该算法表述为一种优化,但也可以给出一种梯度下降式的封闭形式更新[Duchi和Singer, 2009]。Duchi等人将该算法描述为一种特殊的复合物镜下降(COMID)算法[2010b]。
Xiao[2009]的正则对偶平均算法(RDA)如下:
对比FOBOS,RDA是用累积梯度$g_{1:t}$,而不仅仅是$g_t$。我们将在定理4证明当$\lambda=0$以及$l_t$不是强凸时,该算法(RDA)实际上等价于在线自适应梯度下降法(AOGD)[Bartlett et al., 2007]
【原文】

【译文】
FTRL-Proximal算法如下:
该算法在 [McMahan and Streeter, 2010]的论文中有介绍,但是没有支持显示的$\Phi$,而[McMahan, 2011]证明了处理固定$\Phi$函数的更一般算法的遗憾界
我们的主要贡献之一就是展示了这四种算法之间的紧密联系;表1总结了定理2和定理4的关键结果,以使与RDA和FTRL-Proximal的关系显式的形式编写了AOGD和FOBOS。
【原文】

【译文】
在我们的分析中,我们将用任意凸函数$R_t$和$\hat{R_t}$来代替上面出现的$\frac{1}{2}||Q_t^{1/2}x||_2^2$和$\frac{1}{2}||Q_t^{1/2}(x-x_t)||_2^2$,同时用任意凸函数$\Phi(x)$代替$\lambda||x||_1$。对这些算法,矩阵$Q_t$被自适应的选择。我们在实验中使用per-coordinate adaptation例如$Q_t$是形如$Q_{1:t}=diag(\hat{\sigma_{t,1}},…,\hat{\sigma_{t,n}})$的对角矩阵,其中$\hat{\sigma_{t,i}}=\frac{1}{\gamma}\sqrt{\sum_{s=1}^t{g_{t,i}^2}}$,详情请见McMahan and Streeter [2010] and Duchi et al. [2010a]。由于所有算法都受益于这种方法,因此即使在大多数情况下以标量学习率引入它们,我们也使用原始算法的更熟悉的名称。 是学习率比例参数,我们在实验中对其进行了调整。
【原文】

【译文】
高效的实施度:所有这些算法都可以有效实施,因为$g_t$的更新能在$O(K)$时间内完成,其中$K$非零。FTRL-Proximal和RDA可以通过存储每个属性的两个积分值,一个二次项和一个线性项来实现(对角学习率)。 当需要$x_{t,i}$时,可以用封闭形式的懒惰式求解(例如参见[Xiao,2009])。
对FOBOS来说,更新中$\lambda||x||_1$的存在意味着所有系数$x_{t.i}$(即使在$g_{t,i}=0$时也)需要更新。然而,但是,通过存储$g_{t,i}$不为零的最后一轮的索引t,L1 的一部分更新是懒惰的[Duchi and Singer,2009]。
【原文】

【译文】
可行集: 在某些应用中,我们可能只用来自受限凸可行集$F \sub R^n$的点,例如,图中两个节点之间的路径集。由于我们考虑的所有算法都支持复合更新,因此可以通过选择在$F$上的指标函数$\Phi_F$来选择$\Phi$来完成更新,也就是$\Phi_F(x)=0 , if(x \in F),else(\infty)$。可以直接证明$\arg\min_{x\in R^n}{g_{1:t}x+R_{1:t}(x)+\Phi_F(x)}$等价于$\arg\min_{x\in F}{g_{1:t}x+R_{1:t}(x)}$,并且我们无需明确讨论$F$,而是考虑任意扩展的凸函数,就可以推广特定可行集的结果[McMahanand Streeter, 2010]
【原文】


【译文】
我们记$x,y\in R^n$的内积为$x^Ty,or,xy$。$x_{t,i}\in R$表示时间$t$的第$i$个变量。$B$是半正定矩阵,有$||B^{1/2}x||_2^2=x^TBx$。除非另有说明,否则假定凸函数是域$R^n$和范围$R^n\cup\{\infty\}$的扩展。对凸函数$f$,$\partial{f}$表示$f$在$x$上的导数。通过定义,对所有$y$,有$f(y)\ge f(x)+g^T(y-x)$,其中$g\in \partial f(x)$。当$f$可导时,记$\nabla f(x)$为$f$在$x$的导数。这种情况下,$\partial f(x) = \{\nabla f(x)\}$。除非特别指定,不然所有的$mins$和$argmins$都是在$R^n$上。我们经常使用以下标准结果,总结如下:
【原文】
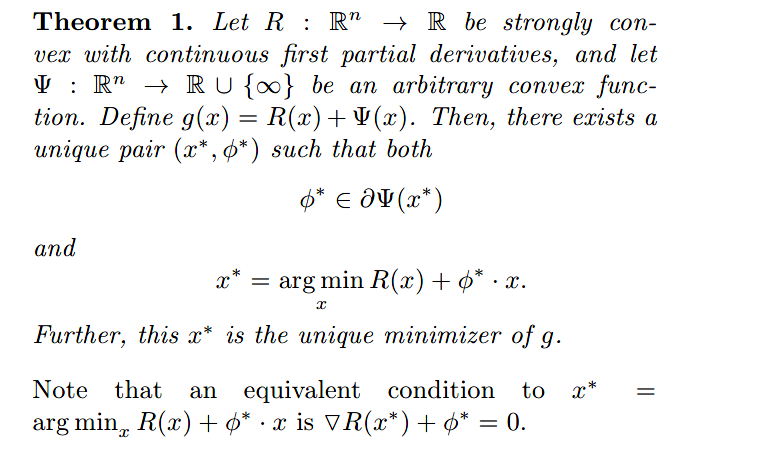
【译文】
定理1:令$R:R^n \rightarrow R$是具有连续一阶偏导数的强凸函数以及令$\Psi:R^n \rightarrow R\cup \{\infty\}$是任意凸函数。定义$g(x)=R(x)+\Psi(x)$。则,存在一个如下等式的唯一对$(x^*,\phi^*)$:
且$x^*$是$g$的唯一最小值。
【证明】

【译文】
由于$R$是强凸的,所以$g$也是强凸的。则$g$拥有唯一最小值$x^*$。令$r=\nabla R$,则存在$\phi^* \in \partial \Psi(x^*)$使得$r(x^*)+\phi^*=0$(因为这是$0\in \partial g(x^*)$的必要充分条件)。且$x^*=\arg_x\min{R(x)+\phi^*x}$(因为$r(x^*)+\phi^*$是其在$x^*$处的梯度)。假定有另外一组$(x^1,\phi^1)$满足这个定理,即$r(x^{1})+\phi^{1}=0$以及$0 \in \partial g(x^1)$,且$x^1$是$g$的唯一最小值。由于最小值是唯一的,则$x^1=x^*,\phi^1=-r(x^*)=\phi^*$。
2 MIRROR DESCENT FOLLOWS THE LEADER
【原文】

【译文】
在本节中,我们考虑了镜像下降算法(最简单的示例是在线梯度下降)和FTRL算法之间的关系。令$f_t(x)=g_tx+\Psi(x)$,其中$g_t \in \partial l_t(x_t)$。令$R_1$强凸,所有$R_t$凸。 除非另有说明,否则我们假设$\min_xR_1(x)= 0$,并假设$x = 0$是唯一的最小值。
FTRL
【原文】



【译文】
FTRL:最简单的遵循正规领导算法如下:
对$t=1$,我们通常取$x_1=0$。我们可以将$\frac{1}{2}||x||_2^2$替换成任意强凸函数$R$,如下:
我们可以为每个$t$独立选择$\sigma_{1:t}$,但是需要它是非减的,因此将其写成每轮增量$\sigma_t \ge 0$的总和是合理的。更一般的更新如下:
在每个回合上添加一个额外的凸函数$R_t$。 令$R_t(x)=\sigma_tR(x)$恢复先前的公式(6)。
当$\arg_{x\in R^n}\min{R_t(x)=0}$,我们称函数$R_t$为origin-centered。我们还可以定义$FTRL^1$的proximal版本,将其他正则化放在当前点而不是原点的中心。在这节,我们保留$R_t$的定义并写出其origin-centered函数$\tilde{R}_t(x)=R_t(x-x_t)$。请注意,仅需要$\tilde{R}_t$来选择$x_{t+1}$,并且此时$x_t$是算法已知的,从而确保算法在计算$x_{t+1}$时仅需要访问第一个t损失函数(根据需要)。 一般更新如下:
最简单的情形如下:
Mirror Descent
【原文】

【译文】
Mirror Descent:最简单的mirror descent版本是以同一步长$\eta$的梯度下降算法,如下:
为了得到低惩罚,$T$必须事先知道,以便可以相应的选择$\eta$。但是,由于有一个关于在点$x_{t+1}$上的$g_{1:t}$和$\eta$的封闭形式解决方案,我们将此归纳为一个“revisionist”算法,该算法在每一轮中都扮演着这样的观点:如果在第1到$t-1$轮中使用了步长$\eta_t$,则具有恒定步长的梯度下降将发挥作用。也就是$x_{t+1}=-\eta_tg_{1:t}$。当$R_t(x)=\frac{\sigma_t}{2}||x||_2^2$且$\eta_t=\frac{1}{\sigma_{1:t}}$,这等价于FTRL。
更一般的,我们将对梯度下降算法更感兴趣,该算法使用的自适应步长至少(取决于)轮数$t$。 在每个回合中使用可变步长$t$进行梯度下降如下:
【原文】

【译文】
这种更新的直觉来自于它可以被重写为如下:
这个版本抓住了这样一个概念(在线学习术语),即我们不想过多地改变我们的假设$x_t$(因为害怕对我们已经看到的例子做出错误的预测),但我们确实想朝着减少我们最近看到的例子的假设损失的方向前进(这是由线性函数$g_t$近似得出的)。
【原文】

【译文】
镜像下降算法利用了这种直觉,用任意的Bregman离散收敛替换了$L_2$平方惩罚。对于可微的,严格凸的,响应的Bregman散度为:
对任意的$x,y\in R^n$,我们得到以下更新:
或者更明确地(通过将(14)的梯度设置为0):
其中$r=\nabla R$。令$R(x)=\frac{1}{2}||x||_2^2$以使$\Beta_R(x, x_t)=\frac{1}{2}||x-x_t||_2^2$恢复公式(13)的算法。看到这种情况的一种方式是注意在这种情况下$r(x)=r^{-1}(x)=x$。
【原文】


【译文】
我们可以通过在每一轮的Bergman散度中加入一个新的强凸函数$R_t$来进一步推广它。也就是说,让:
所以更新变成:
或等价于$x_{t+1}=(r_{1:t})^{-1}(r_{1:t}(x_t)-g_t)$,其中$r_{1:t}=\sum_{s=1}^t{\nabla R_t}=\nabla R_{1:t}$以及$(r_{1:t})^{-1}$是$r_{1:t}$的反函数。步长$\eta_t$隐藏编码在$R_t$的选择中。
COMID将$\Psi$函数加入每一轮迭代:$f_t(x)=g_tx+\Psi(x)$。然后更新如下:
可以推广成如下:
其中学习率$\eta$被定义在$R_1,…,R_t$。如果选择$\Psi$作为凸集上的指标函数,则COMID可通过贪婪投影将标准下降到镜面下降。
2.1 An Equivalence Theorem for Proximal Regularization
【原文】

【译文】
在定理2中,我们表明镜像下降算法可以被视为FTRL算法。
定理2:令$R_t$是一组可微分的原点中心凸函数($\nabla R_t(0)=0$),$R_1$是强凸的,且令$\Psi$是任意凸函数。令$x_1=\hat{x}_1=0$。对一组损失函数$f_t(x)=g_tx+\Psi(x)$,在一组点上的复合目标镜像梯度算法如下:
其中$\tilde{R}_t(x)=R_t(x-\hat{x}_t)$,以及$\tilde{\Beta}_t=\Beta_{\tilde{R}_t}$,所以$\tilde{\Beta}_{1:t}$是关于$\tilde{R}_1+··+ \tilde{R}_t$的Bregman散度。考虑在另外一组点$x_t$上的FTRL算法,
其中$\phi_t\in\partial{\Psi(x_{t+1})}$以致于$g_{1:t}+\phi_{1:t-1}+\nabla{\tilde{R}_{1:t}(x_{t+1})}+\phi_t=0$。那么,这些算法是等价的,即对所有$t>0$,有$x_t=\hat{x}_t$。
【原文】

【译文】
镜像下降定理中使用的Bregman散度是关于近端函数$\tilde{R}_{1:t}$,而通常(如方程(17))这些函数将不依赖于之前的点发挥。我们将证明当$R_t(x)=\frac{1}{2}||Q_t^{1/2}x||_2^2$时,这些问题将不存在。考虑任意$\Psi$函数也会使定理陈述有些复杂。以下推论回避了这些复杂性,以陈述简单的直接等价结果
推论3:令$f_t(x)=g_tx$。然后,以下算法发挥相同的作用:
使用半正定学习速率$Q_t$的梯度下降算法:
FTRL算法



