一、CF(Collaborative-Filtering)

主要思想：

协同过滤推荐方法的主要思想是：利用已有用户群过去的行为或意见预测当前用户最可能喜欢哪些东西或对哪些东西感兴趣。

1、基于用户的协同过滤

潜在假设：

• 如果用户过去有相似的偏好，那么他们未来也会有相似的偏好；
• 用户偏好不会随时间而变化

主要思想：

• 首先，给定一个评分数据集和当前用户的ID作为输入，找出与当前用户过去有相似偏好的其他用户；
• 然后，对当前用户没有评价过的物品，利用最近邻对物品的评分计算预测值。

（1）协同推荐的评分数据库（例子1）

（2）算法步骤

• 利用用户已有的物品评分rate计算用户之间的相似度$sim(a, b)$，相似度计算方法可以是pearson相关系数、改进余弦相似度、spearman秩相关系数、均方差等。（计算相似度是用两个用户拥有共同行为物品的评分来计算）
• 针对要预测的每个用户，选择与其相似度排名最靠前的k个用户对指定物品的评分做加权计算来得到该用户对该物品的评分。

（3）面临的挑战

• 用户量和物品量很大时，算法性能不高
• 当需要扫描大量潜在近邻时，很难做到实时计算预测值

2、基于物品的协同过滤

主要思想：

• 利用物品间的相似度来计算预测值

3、疑难解答

1. 相似度的改进=热门item或者活跃user带来的问题

• 参考论文: Empirical Analysis of Predictive Algorithm for Collaborative Filtering
• 改进办法参考博客链接

二、LR(Logistic Regression)+FTRL

1、逻辑回归

FTRL本质上是一种优化方法，最早由google提出并用于CTR预估。常被用于逻辑回归的优化，因此先简单介绍一下逻辑回归的内容。

1.1 sigmoid函数

由于二分类结果是1或者0，这与数学的阶跃函数很类似，但是阶跃函数在x=0的位置会发生突变，这个突变在数学上很难处理。所以一般使用sigmoid函数来拟合：

$$g(z)={\frac 1{1+e^{-z}}} \qquad(1)$$

具体应用到逻辑回归算法中：

$$z={\omega}_0+{\omega}_1x_1+{\omega}_2x_2+......+{\omega}_nx_n=\sum_{i=0}^n{\omega}_ix_i=\mathbf{\omega^TX} \qquad(2)$$

其中$x_i$表示样本属性（对于我们而言，就是标签IP）的值， $\omega_i$表示这个属性对应的系数（也就是算法需要计算的内容）。注意这里将$x_0$与$\omega_0$也代入了上述公式，其中前者恒为1。于是问题就变成了在训练样本中，已知属性x与最终分类结果y（1或者0）时，如何求得这些系数 $\omega_i$，使得损失最小。

1.2 极大似然估计MLE与损失函数

在机器学习理论中，损失函数（loss function）是用来衡量模型的预测值$f(x)$与真实值$Y$的不一致程度，它是一个非负实值函数，损失函数越小，模型越优（还需考虑过拟合等问题）。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项，通常可以表示成如下式子

$$\omega^* = \arg \min_\omega \frac{1}{m}{}\sum_{i=1}^{m} L(y_i, f(x_i; \omega)) + \lambda\ \Phi(\omega) \qquad(3)$$

其中m表示样本的数量。对于逻辑回归，其loss function是log损失，这可以通过极大似然估计进行推导得到。

首先，给定一个样本$x$，可以使用一个线性函数对自变量进行线性组合，即上述的（2）式子：

$$z={\omega}_0+{\omega}_1x_1+{\omega}_2x_2+......+{\omega}_nx_n=\sum_{i=0}^n{\omega}_ix_i=\mathbf{\omega^TX} \qquad(4)$$

根据sigmoid函数，我们可以得出预测函数的表达式为：

$$h_{\omega}(x) = g(\omega^Tx) = \frac{1}{1 + e^{-\omega^Tx}} \qquad(5)$$

上式表示$y=1$的预测函数为$h_{\omega}(x)$。在这里，假设因变量$y$服从伯努利分布，那么可以得到下列两个式子：

$$\begin{aligned} p(y=1 | x) &= h_{\omega} (x) \quad\qquad(6)\\ p(y=0 | x) &= 1 - h_{\omega} (x) \qquad(7) \end{aligned}$$

而对于上面的两个表达式，通过观察，我们发现，可以将其合并为以下表达式：

$$p(y | x) = h_{\omega} (x)^y (1-h_{\omega} (x))^{1-y} \qquad(8)$$

根据上面的式子，给定一定的样本之后，我们可以构造出似然函数，然后可以使用极大似然估计MLE的思想来求解参数。但是，为了满足最小化风险理论，我们可以将MLE的思想转化为最小化风险化理论，最大化似然函数其实就等价于最小化负的似然函数。对于MLE，就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者说是什么样的参数才能使我们观测到目前这组数据的概率最大。使用MLE推导LR的loss function的过程如下。
首先，根据上面的假设，写出相应的极大似然函数（假定有$m$个样本）：

$$\begin{aligned} L(\omega)&= \prod_{i=1}^{m} p(y_i | x_i; \omega) \\ &= \prod_{i=1}^{m} h_{\omega} (x_i)^{y_i} (1-h_{\omega} (x_i)^{1-y_i} \\ \end{aligned} \qquad(9)$$

上述式子中的$\omega$及$x_i$均为向量，并未显示其转置。

直接对上面的式子求导会不方便，因此，为了便于计算，我们可以对似然函数取对数，经过化简可以得到下式的推导结果：

$$\begin{aligned} \log L(\omega)&= \sum_{i=1}^{m} \log \left [ (h_{\omega} (x_i)^{y_i} (1-h_{\omega} (x_i))^{1-y_i}) \right ] \\ &= \sum_{i=1}^{m} \left [ y_i \log h_{\omega} (x_i) + (1-y_i) \log(1-h_{\omega} (x_i)) \right ] \\ \end{aligned} \qquad(10)$$

因此，损失函数可以通过最小化负的似然函数得到，即下式：

$$J(\omega) = - \frac{1}{m} \sum_{i=1}^m \left [ y_i \log h_{\omega}(x_i) + (1-y_i) \log(1-h_{\omega}(x_i) \right ] \qquad(11)$$

在周志华版的机器学习中，将sigmiod函数代入$h_{\omega}(x_i)$，并使用ln代替log，上述公式表示为：

$$\begin{aligned} J(\omega) &= - \frac{1}{m} \sum_{i=1}^m \left [ y_i \ln h_{\omega}(x_i) + (1-y_i) \ln(1-h_{\omega}(x_i) \right ]\\ &=- \frac{1}{m} \sum_{i=1}^m \left [ y_i\ln \frac{1}{1+e^{-\omega x_i}}+(1-y_i)\ln \frac{e^{-\omega x_i}}{1+e^{-\omega x_i}}\right ]\\ &=- \frac{1}{m} \sum_{i=1}^m \left [ \ln \frac{1}{1+e^{\omega x_i}} + y_i \ln \frac{1}{e^{-\omega x_i}}\right ]\\ &= \frac{1}{m} \sum_{i=1}^m \left [ -y_iwx_i + \ln(1+e^{\omega x_i})\right ] \end{aligned} \qquad(12)$$

在某些资料上，还有另一种损失函数的表达形式，但本质是一样的，如下【推导见下面1.4】：

$$J(\omega) = \frac{1}{m} \sum_{i=1}^m log(1 + e^{-y_i \omega x}) \qquad(13)$$

1.3 梯度下降

我们以梯度下降为例对逻辑回归进行求解，其迭代公式的推导过程如下：

$$\begin{aligned} \frac{ \partial J(\omega)} {\partial \omega_j}&= -\frac{1}{m} \sum_{i}^{m} \left [ y_i(1 - h_{\omega}(x_i)) \cdot (-x_{i,j}) + (1 - y_i) h_{\omega} (x_i) \cdot (x_{i,j}) \right ]\\ & = - \frac{1}{m} \sum_{i}^{m} (-y_i \cdot x_{i,j} + h_{\omega}(x_i) \cdot x_{i,j}) \\ & = -\frac{1}{m} \sum_{i}^{m} (h_{\omega}(x_i) - y_i) x_{i,j} \end{aligned} \qquad(14)$$

上述中$x_{i,j}$表示第$i$个样本的第$j$个属性的取值。
于是，$\omega$的更新方式为：

$$\omega_{j+1} = \omega_j - \alpha \sum_{i=1}^{m} (h_{\omega}(x_i) - y_i) x_{x,j}$$

对于随机梯度下降，每次只取一个样本，则$\omega$的更新方式为：

$$\omega_{j+1} = \omega_j - \alpha (h_{\omega}(x)- y) x_{j}$$

其中$x$为这个样本的特征值，$y$为这个样本的真实值，$x_j$为这个样本第$j$个属性的值。

使用周志华版的损失函数更容易得出这个结论。

1.4 另一种形式的损失函数及其梯度

与上面相同，根据sigmoid函数，我们可以得出预测函数的表达式为：

$$h_{\omega}(x) = g(\omega^Tx) = \frac{1}{1 + e^{-\omega^Tx}}$$

上式表示$y=1$的预测函数为$h_{\omega}(x)$。
但与上面不同，我们假设样本的分布为{-1,1}，则

$$p(y=1 | x) = h_{\omega} (x)$$ $$p(y=-1 | x) = 1 - h_{\omega} (x)$$

对于sigmoid函数，有以下特性（简单推导一下就可以得到）：

$$h(-x) = 1 - h(x)$$

于是(14)(15)式可以表示为：

$$p(y|x) = h_\omega(yx)$$

同样，我们使用MLE作估计，

$$\begin{aligned} L(\omega)&= \prod_{i=1}^{m} p(y_i | x_i; \omega) \\ &= \prod_{i=1}^{m} h_\omega(y_i x_i)\\ &= \prod_{i=1}^{m} \frac{1}{1+e^{-y_iwx_i}} \end{aligned}$$

对上式取对数及负值，得到损失为：

$$\begin{aligned} -\log L(\omega)&= -\log \prod_{i=1}^{m} p(y_i | x_i; \omega) \\ &= -\sum_{i=1}^{m} \log p(y_i | x_i; \omega) \\ &= -\sum_{i=1}^{m} \log \frac{1}{1+e^{-y_iwx_i}}\\ &= \sum_{i=1}^{m} \log(1+e^{-y_iwx_i})\\ \end{aligned}$$

即对于每一个样本，损失函数为：

$$L(\omega)=\log(1+e^{-y_iwx_i})$$

对上式求梯度，容易得到：

$$\begin{aligned} \frac{ \partial J(\omega)} {\partial \omega_j}&= \frac{-y_i x_i}{1+e^{y_i \omega x_i}} \end{aligned}$$

2、FOBOS与RDA

2.1 FOBOS基本原理

FOBOS算法由John Duchi和Yoram Singer提出，是梯度下降的一个变种。
与梯度下降不同，它将权重的更新分为2个步骤：

$$\begin{aligned} W_{t+\frac{1}{2}}&=W_t-\eta_tG_t \\n W_{t+1}&=\arg\min\{\frac{1}{2}\|W-W_{t+\frac{1}{2}}\|^2+\eta_{(t+\frac{1}{2})}\psi(W)\} \end{aligned}$$

从上面的2个步骤可以看出：
第一个步骤是一个标准的梯度下降。
第二个步骤是对梯度下降的结果进行微调。这里可以分为2部分：（1）前半部分保证了微调发生在第一个步骤结果（取梯度下降结果）的附近。（2）后半部分用于处理正则化，产生稀疏性。

根据次梯度理论的推断，可以得出$W_{(t+1)}$不仅仅与迭代前的状态$W_t$有关，而且与迭代后的相关

2.2 L1-FOBOS

FOBOS在L1正则化条件下，特征权重的更新方式为：（推导过程暂略）

$$\omega_{t+1,i}=sgn(\omega_{t,i}-\eta_tg_{t,i})max\{0,|\omega_{t,i}-\eta_tg_{t,i}|-\eta_{t+\frac{1}{2}}\lambda\}$$

其中$g_{t,i}$为梯度在维度i上的取值

2.3 RDA基本原理

简单截断、TG、FOBOS都是建立在SGD基础上的一个变种，属于梯度下降类型的方法，这类方法的精度比较高，同时也能得到一定的稀疏性。而RDA是从另一个方面来求解，它的精度比FOBOS等略差，但它更有效的提升了稀疏性。

在RDA中，特征权重的更新策略为：

$$W_{t+1}=\arg\min\{\frac{1}{t}\sum_{r=1}^{t}<G^{r},W>+\psi(W)+\frac{\beta_t}{t}h(W)\}$$

其中$<G^{r},W>$表示梯度$G^r$对W的积分平均值（积分中值）；$\psi(W)$为正则项；$h(W)$为一个辅助的严格的凸函数；${\beta_t|t\ge1}$是一个非负且非自减序列。

2.4 L1-RDA

在L1正则化条件下，RDA的各个维度的权重更新方式为：

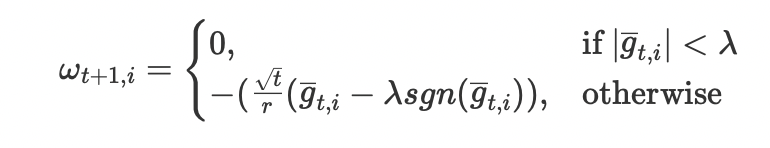
亦即当某个维度上的累积梯度平均值的绝对值 $|\overline g_{t,i}|$小于阈值$\lambda$时，该维度权重被置为0。

3、FTRL

理论及实验均证明，L1-FOBOS这类基于梯度下降的算法有比较高的精度，但L1-RDA却能在损失一定精度的情况下产生更好的稀疏性。
把这二者的优点结合成一个算法，这就是FTRL算法的来源。

3.1 从L1-FOBOS和L1-RDA推导FTRL

我们令$\eta_{t+\frac{1}{2}}=\eta_t=\Theta(\frac{1}{\sqrt{t}})$是一个非增正序列，同时代入L1正则项，得到L1-FOBOS的形式如下：

$$\begin{aligned} W_{t+\frac{1}{2}}&=W_t-\eta_tG_t \\ W_{t+1}&=\arg\min\{\frac{1}{2}\|W-W_{t+\frac{1}{2}}\|^2+\eta_{t}\lambda\|W\|_1\} \end{aligned}$$

将这2个公式合并到一起，得到L1-FOBOS的形式如下：

$$W_{t+1}=\arg\min\{\frac{1}{2}\|W-W_t+\eta_tG_t\|^2+\eta_{t}\lambda\|W\|_1\}$$

将上式分解为N个独立的维度进行最优化求解：

$$\begin{aligned} w_i&=\arg\min\{\frac{1}{2}\|w_i-w_{t,i}+\eta_tg_{t,i}\|^2+\eta_{t}\lambda|w_{t,i}|_1\} \\ &=\arg\min\{\frac{1}{2}(w_i-w_{t,i})^2+\frac{1}{2}(\eta_t g_{t,i})^2+w_i\eta_tg_{t,i}-w_{t,i}\eta_tg_{t,i}+\eta_t\lambda|w_i|\}\\ &=\arg\min\{w_ig_{t,i}+\lambda|w_i|+\frac{1}{2\eta_t}(w_i-w_{t,i})^2+|\frac{\eta_t}{2}g_{t,i}^2-w_{t,i}g_{t,i}|\} \end{aligned}$$

• 上述推导的最后一步是通过除以$\eta_t$得到的。
  由于上式中的最后一项$|\frac{\eta_t}{2}g_{t,i}^2-w_{t,i}g_{t,i}|$是一个与$w_i$无关的量，因此上式可简化为： $$w_i=\arg\min\{w_ig_{t,i}+\lambda|w_i|+\frac{1}{2\eta_t}(w_i-w_{t,i})^2\}$$ 把N个独立优化的维度重新合并，L1-FOBOS可写成以下形式： $$W_{t+1}=\arg\min\{G_tW+\lambda\|W\|_1+\frac{1}{2\eta_t}\|W-W_t\|_2^2\}$$

另一方面，L1-RDA可以表达为：

$$W_{t+1}=\arg\min\{G_{(1:t)}W+t\lambda\|W\|_1+\frac{1}{2\eta_t}\|W-0\|_2^2\}$$

其中$G_{(1:t)}=\sum_{s=1}{t}G_s$。
我们令$\sigma_s=\frac{1}{\eta_s}-\frac{1}{\eta_{s-1}}$，可以得到$\sigma_{(1:t)}=\frac{1}{\eta_t}$。那么L1-FOBOS与L1-RDA可以写为以下格式：

$$\begin{aligned} W_{t+1}&=\arg\min\{G_tW+\lambda\|W\|_1+\frac{1}{2}\sigma_{(1:t)}\|W-W_t\|_2^2\}\\ W_{t+1}&=\arg\min\{G_{(1:t)}W+t\lambda\|W\|_1+\frac{1}{2}\sigma_{(1:t)}\|W-0\|_2^2\} \end{aligned}$$

比较以上2式的区别：

• （1）L1-FOBOS考虑的是当前梯度的影响，L1-RDA则考虑了累积影响。
• （2）L1-FOBOS限制$W_{t+1}$不能离$W_t$太远，而L1-RDA的W则不能离0太远，因此后者更容易产生稀疏性。

3.2 FTRL权重更新的最终形式

在google2010公布的理论文章中并没有使用L2正则项，但在2013年公布工程实施方案时引入了L2。
因此，综合上述的L1-FOBOS及L1-RDA，FTRL算法的权重更新方式为：

$$W_{t+1}=\arg\min\{G_{(1:t)}W+\lambda_1\|W\|_1+\lambda_2\|W\|_2^2+\frac{1}{2}\sum_{s=1}^t(\sigma_s\|W-W_s\|_2^2)\}$$

将上式展开，得到

$$W_{t+1}=\arg\min\{(G_{(1:t)}-\sum_{s=1}^t\sigma_sW_s)W+\lambda_1\|W\|_1+\frac{1}{2}(\lambda_2+\sum_{s=1}^t\sigma_s)\|W\|^2+\frac{1}{2}\sum_{s=1}^{t}\sigma_s\|W_s\|_2^2\}$$

由于上式的最后一项相对于W来说是一个常数，同时令$Z_t=G_{(1:t)}-\sum_{(s=1)}^t\sigma_sW_s$，上式可表示为：

$$W_{t+1}=\arg\min\{Z_tW+\lambda_1\|W\|_1+\frac{1}{2}(\lambda_2+\sum_{s=1}^t\sigma_s)\|W\|^2\}$$

各个维度可以独立表示为：

$$w_{i+1}=\arg\min\{z_{t,i}w_i+\lambda_1|w_i|+\frac{1}{2}(\lambda_2+\sum_{s=1}^{t}\sigma_s)w_i^2\}$$

使用与L1-FOBOS相同的分析方法可以得到：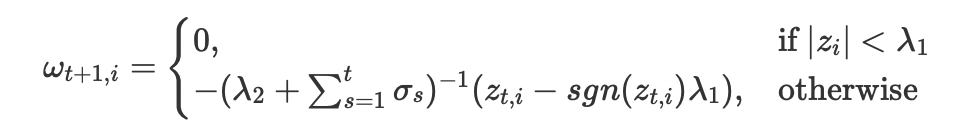

根据上面的定义:

$$\sigma_{(1:t)}=\sum_{s=1}^t\sigma_s=\frac{1}{\eta_t}$$

我们使用下面介绍的学习率，以及令$n_i=\sum g_i^2$，则可以得到FTRL的最终形式：

3.3 学习率

1、per-coordinate learning rate
在FTRL中，学习率的定义如下：

$$\eta_{t,i}=\frac{\alpha}{\beta+\sqrt{\sum_{s=1}^tg_{s,i}^2}}$$

其中$\alpha\beta$是自定义的参数。

在一般梯度下降算法中，使用的是一个全局的学习率策略：$\eta_t=\frac{1}{\sqrt{t}}$。这个策略保证了学习率是一个正的非增序列，这个值对于每一个特征都是一样的。

考虑一个极端的情况，我们有多个稀疏特征，其中一个特征$x_1$出现非常频繁，而另一个特征$x_2$很少出现。比如第一个样本，$x_1$和$x_2$同时出现了，但接下来的99个样本都只出现了$x_1$，然后第100个样本$x_2$又出来了，由于此时的学习率为$\frac{1}{\sqrt{100}}$，远小于第一个样的影响了。也就是说假如第一个样本是正样本，第10个样本是负样本，此时由于学习率的不同，模型会认为$x_2$会是一个有用的正相关的特征，即$\omega>0$。但事实上，这个特征只出现了2次，而且一正一负，因此这应该是一个无用的特征，即$\omega=0$。

在FTRL中，我们会使用一个特征的累积梯度，由于中间的99个数据没有这个特征，因此其对应的梯度为0，因此第二次的负样本对应的学习率只是略小于第一个正样本。

3.4 工程实现计算过程

3.4.1 一些定义

对于每一个样本，我们计算以下数值。

（1）$p_t$

使用当前的$\omega$代入sigmoid函数得出的预测值，即：

$$p=\frac{1}{1+e^{-(\sum_{i=1}^n\omega_ix_i)}}$$

（2）$g_i$

损失函数在某一个维度上的梯度，对于逻辑回归而言：

$$g_i=(p-y)x_i$$

其中y为当前样本的实际值，即0或者1。

（3）$n_i$

这是该维度梯度$g_i^2$的累积值，即：

$$n_i=n_i+g_i^2$$

（4）$\eta_i$

这是该维度的学习率，它与累积梯度有关。定义为：

$$\eta_i=\frac{\alpha}{\beta+\sqrt{\sum_{s=1}^t(g_i^s)^2}}=\frac{\alpha}{\beta+\sqrt{n_i}}$$

其中$\alpha\beta$为用户定义的2个参数。

（5）$\sigma_i$

其中$\sigma_i$是一个中间计算值，没有实际含义，其定义为：

$$\sigma_i=\frac{1}{\eta_{t,i}}-\frac{1}{\eta_{t-1,i}}=\frac{1}{\alpha}(\sqrt{n_i+g_i^2}-\sqrt{n_i})$$

（6）$z_i$

其中$z_i$也是一个辅助计算的中间值，它的定义为：

$$z_{t,i}=g^{(1:t)}-\sum_{s=1}^t{\sigma_{s,i}\omega_{s,i}}$$

于是$z_i$的更新为：

$$z_t-z_{t-1}=g_t-\sigma_{t}\omega_{t}$$

即：

$$z_i=z_i+g_t-\sigma_i\omega_i$$

3.4.2 FTRL算法

（1）设定以下4个输入参数，这些参数根据经验而定，可以参考以下数据：

$$\alpha=0.1,\beta=1,\lambda_1=1,\lambda_2=1$$

（2）初始化以下数值：

$$z_i=0,n_i=0$$

（3）对于每一个样本的所带的每一个维度,更新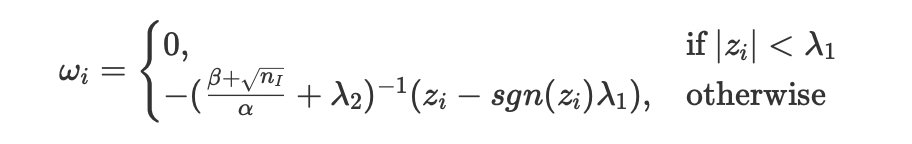$\omega$

（4）使用上面更新后的$\omega$，预测这个样本的值，即代入sigmoid函数计算$p_t$

$$p=\frac{1}{1+e^{-(\sum_{i=1}^n\omega_ix_i)}}$$

（5）对于每一个样本的每一个维度，更新$g_i,\sigma_i,z_i,n_i$，即上面所说的：

$$\begin{aligned} g_i&=(p-y)x_i \\ \sigma_i&=\frac{1}{\alpha}(\sqrt{n_i+g_i^2}-\sqrt{n_i})\\ z_i&=z_i+g_t-\sigma_i\omega_i\\ n_i&=n_i+g_i^2 \end{aligned}$$

3.4.3 特征的独立性

如果特征是非独立的，会导致特征的权重不符合预期。
比如，有2个特征A和B，然后加了一个组合标签A&B，假如A和B都是和label非常正相关的，A&B效果更好。但结果会发现A&B这个标签的权重值可能还不如A或者B的权重高。
这是因为，带了A&B标签的，必然带A或者B，大概率被预测成高概率值，而LR梯度为：

$$(p-y)x_i$$

对于正样本，$y=1$，则梯度并不大，所以A&B提升并不大；而对于负样本，$y=0$，则梯度非常大，导致惩罚很大，权重降低很多。

所以最终结果A和B的权重都可能比A&B要大，但对于带A&B标签的用户来说，他由于同时带3个特征，所以预测概率值还是比较高的。

当然最好的办法是尽量避免这种关联性太强的特征。

4、FTRL的工程应用

这里只列出了google提供的一些建议，我们自身的工程应用并不包含在内。

（1）减少样本的数量

• Poisson Inclusion：以p的概率接受样本
• Bloom Filter Inclusion：只有当特征出现次数达到一定数量后，特征才会被加入模型

（2）使用更少的位来进行浮点数编码
一般而言，特征对应的$\omega$在(-2,2)之间，所以我们可以将32，或者64位的浮点数编码规则改为q2.13编码方式，即2位整数，1位小数点，13位小数。

（3）多个类似的模型
把多个同类型/相似的模型放在一起保存，可以不需要记录多个key，只需要记录一次Key，以及各个模型中的$\omega$。这可以节省内存、带宽、CPU、存储。

（4）只保存一个模型
在上面的基础上更进一步，所有模型共用一份$\omega$，以及以一个bit来记录本模型有哪些特征。当模型更新某个$\omega$后，取它与之前那个值的平均值。
与共用一个模型对比，好处是记录了这个模型有哪些有效特征，共用模型就无法区分了。

（5）近似计算学习率
只使用正样本P与负样本数据N来近似估计梯度的平方和，前提是假设特征有类似的分布。

$$\sum{g_i^2}=\frac{PN}{P+N}$$

（6）减少负样本数量
减少负样本数量，然后在训练时弥补其损失。

三、FM(Factorization Machine)

1.1 背景

1.1.1 线性模型

常见的线性模型，比如线性回归、逻辑回归等，它只考虑了每个特征对结果的单独影响，而没有考虑特征间的组合对结果的影响。

对于一个有n维特征的模型，线性回归的形式如下：

$$\begin{aligned} f(x) &= \omega_0 + \omega_1x_1+\omega_2x_2+...+\omega_nx_n \\ &=\omega_0+\sum_{i=1}^n{\omega_ix_i} \end{aligned} \qquad (1)$$

其中$(\omega_0,\omega_1...\omega_n)$为模型参数，$(x_1,x_2...x_n)$为特征。
从(1)式可以看出来，模型的最终计算结果是各个特征的独立计算结果，并没有考虑特征之间的相互关系。

举个例子，我们认为“USA”与”Thanksgiving”，”China”与“Chinese new year”这样的组合特征是很有意义的，在这样的组合特征下，会对某些商品表现出更强的购买意愿，而单独考虑国家及节日都是没有意义的。

1.1.2 二项式模型

我们在（1）式的基础上，考虑任意2个特征分量之间的关系，得出以下模型：

$$f(x)=\omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n\omega_{ij}x_ix_j \qquad (2)$$

这个模型考虑了任意2个特征分量之间的关系，但并未考虑更高阶的关系。
模型涉及的参数数量为：

$$1+n+\frac{n(n-1)}{2}=\frac{1}{2}(n^2+n+2) \qquad (3)$$

对于参数$\omega_i$的训练，只要这个样本中对应的$x_i$不为0，则可以完成一次训练。
但对于参数$\omega_{ij}$的训练，需要这个样本中的$x_i$和$x_j$同时不为0，才可以完成一次训练。
在数据稀疏的实际应用场景中，二次项$\omega_{ij}$的训练是非常困难的。因为每个$\omega_{ij}$都需要大量$x_i$和$x_j$都不为0的样本。但在数据稀疏性比较明显的样本中，$x_i$和$x_j$都不为0的样本会非常稀少，这会导致$\omega_{ij}$不能得到足够的训练，从而不准确。

1.2 FM

1.2.1 FM基本原理

为了解决二项式模型中由于数据稀疏引起的训练不足的问题，我们为每个特征维度$x_i$引入一个辅助向量：

$$V_i = (v_{i1},v_{i2},v_{i3},...,v_{ik})^T\in \mathbb R^k, i=1,2,3,...,n \qquad(4)$$

其中$k$为辅助变量的维度，依经验而定，一般而言，对于特征维度足够多的样本，$k<<n$。
将$\omega_{ij}$表示为：

$$\omega_{ij}=V_i^TV_j=\sum_{l=1}^kv_{il}v_{jl} \qquad(5)$$

简单的说，我们不再简单的使用样本训练具体的$\omega_{ij}$，而是先训练2个隐变量$V_i$以及$V_j$，然后使用式（5）求出最终的$\omega_{ij}$。

具体而言，$\omega_{ij}=V_i^TV_j$与$\omega_{hi}=V_h^TV_i$有相同的项$V_i$，也就是只要样本中的$x_i$不为0，且最少具有一个其它特征，则这个样本则可用于训练$V_i$，这就解决了数据稀疏性导致的问题。

于是，在FM中，模型可以表达为：

$$f(x) = \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j \qquad(6)$$

1.2.2 数据分析

我们的目标是要求得以下交互矩阵W：

$$W= \begin{pmatrix} \omega_{11} & \omega_{12}& ... &\omega_{1n} \\ \omega_{21} & \omega_{22}& ... &\omega_{2n} \\ \vdots &\vdots &\ddots &\vdots\\ \omega_{n1} & \omega_{n2}& ... &\omega_{nn} \\ \end{pmatrix}_{n\times n} \qquad(7)$$

由于直接求解W不方便，因此我们引入隐变量V：

$$V= \begin{pmatrix} v_{11} & v_{12}& ... &v_{1k} \\ v_{21} & v_{22}& ... &v_{2k} \\ \vdots &\vdots &\ddots &\vdots\\ v_{n1} & v_{n2}& ... &v_{nk} \\ \end{pmatrix}_{n\times k}=\begin{pmatrix} V_1^T\\ V_2^T\\ \cdots \\ V_n^T\\ \end{pmatrix} \qquad(8)$$

令

$$VV^T = W \qquad(9)$$

如果我们先得到V，则可以得到W了。
现在只剩下一个问题了，是否一个存在V，使得上述式（9）成立。
理论研究表明：当k足够大时，对于任意对称正定的实矩阵$W\in \mathbb R^{n \times n}$，均存在实矩阵$V\in \mathbb R^{n \times k}$，使得$W=VV^T$。

理论分析中要求参数k足够的大，但在高度稀疏数据的场景中，由于 没有足够的样本，因此k通常取较小的值。事实上，对参数$k$的限制，在一定程度上可以提高模型的泛化能力。

1.2.3参数个数

假设样本中有n个特征，每个特征对应的隐变量维度为k，则参数个数为$1+n+nk$。
正如上面所言，对于特征维度足够多的样本，$k<<n$。

1.2.4 计算时间复杂度

下面我们分析一下已经知道所有参数，代入式（6）计算预测值时的时间复杂度。从式（6）中一看，

$$f(x) = \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j \qquad(6)$$

可以看出时间复杂度是$O(kn^2)$。但我们对上述式子的最后一项作变换后，可以得出一个$O(kn)$的时间复杂度表达式。

$$\begin{aligned} \sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j &= \frac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n(V_i^TV_j)x_ix_j-\sum_{i=1}^n(V_i^TV_i)x_ix_i\right) \\ &=\frac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n\sum_{l=1}^kv_{il}v_{jl}x_ix_j-\sum_{i=1}^n\sum_{l=1}^k v_{il}^2x_i^2\right)\\ &=\frac{1}{2}\sum_{l=1}^k\left(\sum_{i=1}^n(v_{il}x_i)\sum_{j=1}^n(v_{jl}x_j)-\sum_{i=1}^nv_{il}^2x_i^2\right)\\ &=\frac{1}{2}\sum_{l=1}^k\left(\left(\sum_{i=1}^n(v_{il}x_i)\right)^2-\sum_{i=1}^nv_{il}^2x_i^2\right) \end{aligned} \qquad(10)$$

上述式子中的$\sum_{i=1}^n(v_{il}x_i)$只需要计算一次就好，因此，可以看出上述模型的复杂度为$O(kn)$。
也就是说我们不要直接使用式（6）来计算预测结果，而应该使用式（10），这样的计算效率更高。

1.2.5 梯度

FM有一个重要的性质：multilinearity：若记$\Theta=(\omega_0,\omega_1,\omega_2,...,\omega_n,v_{11},v_{12},...,v_{nk})$表示FM模型的所有参数，则对于任意的$\theta \in \Theta$，存在与$\theta$无关的$g(x)$与$h(x)$，使得式（6）可以表示为：

$$f(x) = g(x) + \theta h(x) \qquad(11)$$

从式（11）中可以看出，如果我们得到了$g(x)$与$h(x)$，则对于参数$\theta$的梯度为$h(x)$。下面我们分情况讨论。

• 当 $\theta=\omega_0$时，式（6）可以表示为：

  $$f(x) = \color{blue}{\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j} +\omega_0 \times \color{red}{1} \qquad(12)$$

  上述中的蓝色表示$g(x)$，红色表示$h(x)$。下同。
  从上述式子可以看出此时的梯度为1.

• 当$\theta=\omega_l, l \in (1,2,...,n)$时，

  $$f(x) = \color{blue}{\omega_0+\sum_{i=1,\ i \ne l}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j}+\omega_l \times \color{red}{x_l} \qquad(13)$$

  此时梯度为$x_l$。

• 当$\theta=v_{lm}$时

  $$f(x) =\color{blue}{ \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(\sum_{s=1 , is \ne lm ,js \ne lm}^k v_{is}v_{js})x_ix_j }+v_{lm}\times \color{red}{x_l\sum_{i=1,i \ne l }^n v_{im}x_i} \qquad(14)$$

  此时梯度为$x_l\sum_{i \ne l } v_{im}x_i$。

综合上述结论，$f(x)$关于$\theta$的偏导数为：

$$\frac{\partial f(x)}{\partial \theta} = \begin{cases} 1, & \theta=\omega_0 \\ x_l, & \theta=\omega_l, l \in (1,2,...,n) \\ x_l\sum_{i=1,i \ne l }^n v_{im}x_i & \theta=v_{lm} \end{cases} \qquad(15)$$

1.2.6 训练时间复杂度

由上述式（15）可以得到：

$$x_l\sum_{i=1,i \ne l }^n v_{im}x_i = x_l\sum_{i=1}^n v_{im}x_i-v_{lm}x_l^2 \qquad(16)$$

对于上式中的前半部分$\sum_{i=1}^n v_{im}x_i$，对于每个样本只需要计算一次，所以时间复杂度为$O(n)$，对于k个隐变量的维度分别计算一次，则复杂度为$O(kn)$。其它项的时间复杂度都小于这一项，因此，模型训练的时间复杂度为$O(kn)$。

详细一点解释：
（1）我们首先计算$\sum_{i=1}^n v_{im}x_i$，时间复杂度为n，这个值对于所有特征对应的隐变量的某一个维度是相同的。我们设这值为C。

（2）计算每一个特征对应的$x_l\sum_{i=1}^n v_{im}x_i-v_{lm}x_l^2 =Cx_l-v_{lm}x_l^2$，由于总共有n个特征，因此时间复杂度为n，至此，总的时间复杂度为n+n。

（3）上述只是计算了隐变量的其中一个维度，我们总共有k个维度，因此总的时间复杂度为$k(n+n)=O(kn)$.

四、FFM(Field Factorization Machine)

2.1 背景及基本原理

在FM模型中，每一个特征会对应一个隐变量，但在FFM模型中，认为应该将特征分为多个field，每个特征对应每个field分别有一个隐变量。

举个例子，我们的样本有3种类型的字段：publisher, advertiser, gender，分别可以代表媒体，广告主或者是具体的商品，性别。其中publisher有5种数据，advertiser有10种数据，gender有男女2种，经过one-hot编码以后，每个样本有17个特征，其中只有3个特征非空。

如果使用FM模型，则17个特征，每个特征对应一个隐变量。
如果使用FFM模型，则17个特征，每个特征对应3个隐变量，即每个类型对应一个隐变量，具体而言，就是对应publisher, advertiser, gender三个field各有一个隐变量。

2.2模型与最优化问题

2.2.1 模型

根据上面的描述，可以得出FFM的模型为：

$$f(x) = \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{j1=1}^{n-1}\sum_{j2=j1+1}^n(V_{j1,f2}^TV_{j2,f1})x_{j1}x_{j2} \qquad(17)$$

其中$j1,j2$表示特征的索引。我们假设$j1$特征属于$f1$这个field，$j2$特征属于$f2$这个field，则$V_{j1,f2}$表示$j1$这个特征对应$f2$($j2$所属的field)的隐变量，同时$V_{j2,f1}$表示$j2$这个特征对应$f1$($j1$所属的field)的隐变量。

事实上，在大多数情况下，FFM模型只保留了二次项，即：

$$\phi(V,x) = \sum_{j1=1}^{n-1}\sum_{j2=j1+1}^n(V_{j1,f2}^TV_{j2,f1})x_{j1}x_{j2} \qquad(18)$$

2.2.2 最优化问题

根据逻辑回归的损失函数及分析，可以得出FFM的最优化问题为：

$$\min \frac{\lambda}{2}||V||_2^2+\sum_{i=1}^{m}\log(1+exp(-y_i\phi(V,x))) \qquad(19)$$

上面加号的前面部分使用了L2范式，后面部分是逻辑回归的损失函数。m表示样本的数量，$y_i$表示训练样本的真实值（如是否点击的-1/1），$\phi(V,x)$表示使用当前的V代入式（18）计算得到的值。

注意，以上的损失函数适用于样本分布为{-1,1}的情况。

2.2.3 自适应学习率

与FTRL一样，FFM也使用了累积梯度作为学习率的一部分，即：

$$V_{j1,f2} = V_{j1,f2} - \frac{\eta}{\sqrt{1+\sum_t(g_{v_{j1,f2}}^t)^2}}g_{v_{j1,f2}} \qquad(20)$$

其中$g_{v_{j1,f2}}$表示对于$V_{j1,f2}$这个变量的梯度向量，因为$V_{j1,f2}$是一个向量，因此$g_{v_{j1,f2}}$也是一个向量，尺寸为隐变量的维度大小，即k。
而$\sum_t(g_{v_{j1,f2}}^t)^2$表示从第一个样本到当前样本一直以来的累积梯度平方和。

2.2.4 FFM算法的最终形式

$$\begin{aligned} (V_{j1,f2})_d &=(V_{j1,f2})_{d-1}-\frac{\eta}{\sqrt{(G_{j1,f2})_d}} \cdot (g_{j1,f2})_d \\ (V_{j2,f1})_d &=(V_{j2,f1})_{d-1}-\frac{\eta}{\sqrt{(G_{j2,f1})_d}} \cdot (g_{j2,f1})_d \end{aligned}$$

其中G为累积梯度平方：

$$(G_{j1,f2})_d=(G_{j1,f2})_{d-1}+(g_{j1,f2})_d^2 (G_{j2,f1})_d=(G_{j2,f1})_{d-1}+(g_{j2,f1})_d^2$$

g为梯度，比如$g_{j1,f2}$为$j1$这个特征对应$f2$这个field的梯度向量：

$$g_{ji,f2}=\lambda \cdot V_{ji,f2} + \kappa \cdot V_{j2,f1} g_{j2,f1}=\lambda \cdot V_{j2,f1} + \kappa \cdot V_{j1,f2}$$

其中$\kappa$为：

$$\kappa=\frac{\partial\log(1+exp(-y_i\phi(V,x))) }{\partial \phi(V,x) }=\frac{-y}{1+\exp(y\phi(V,x) )}$$

2.3完整算法流程

使用随机梯度下降（SGD）训练FFM模型的完整过程如下：

2.3.1 计算梯度

对于每一个样本的每一对特征组合都要计算以下梯度向量。

$$\begin{aligned} g_{ji,f2}=\lambda \cdot V_{ji,f2} + \kappa \cdot V_{j2,f1} \\ g_{j2,f1}=\lambda \cdot V_{j2,f1} + \kappa \cdot V_{j1,f2} \end{aligned} \qquad(21)$$

其中$\kappa$为式(19)后半部分对应的梯度，即：

$$\kappa=\frac{\partial\log(1+exp(-y_i\phi(V,x))) }{\partial \phi(V,x) }=\frac{-y}{1+\exp(y\phi(V,x) )} \qquad(22)$$

再重申一次，$g$与$V$都是k维的向量，在python中可以作为一个向量计算，在java/c++等需要通过一个循环进行计算。

详细推导（21）式如下：
（1）在SGD中，式（19）可以转化为：

$$\min \frac{\lambda}{2}||V||_2^2+\log(1+exp(-y_i\phi(V,x))) \qquad(23)$$

（2）上式对$V_{j1,f2}$求偏导，可得：

$$\begin{aligned} &\frac{\partial \frac{\lambda}{2}||V||_2^2+\log(1+exp(-y_i\phi(V,x)))}{\partial V_{j1,f2}} \\ &=\lambda \cdot V_{j1,f2} + \frac{\partial \log(1+exp(-y_i\phi(V,x)))}{\partial V_{j1,f2}}\\ &=\lambda \cdot V_{j1,f2} + \frac{\partial \log(1+exp(-y_i\phi(V,x)))}{\partial \phi} \cdot \frac{\partial \phi}{V_{j1,f2}}\\ &=\lambda \cdot V_{j1,f2} + \frac{-y}{1+\exp(y\phi(V,x) )} \cdot V_{j2,f1} \end{aligned} \qquad(24)$$

2.3.2 计算累积梯度平方和

计算从第一个样本，到当前样本（第d个）以来的累积梯度平方和：

$$\begin{aligned} (G_{j1,f2})_d=(G_{j1,f2})_{d-1}+(g_{j1,f2})_d^2 \\ (G_{j2,f1})_d=(G_{j2,f1})_{d-1}+(g_{j2,f1})_d^2 \end{aligned} \qquad(26)$$

2.3.3 更新隐变量

$$\begin{aligned} (V_{j1,f2})_d=(V_{j1,f2})_{d-1}-\frac{\eta}{\sqrt{(G_{j1,f2})_d}} \cdot (g_{j1,f2})_d\\ (V_{j2,f1})_d=(V_{j2,f1})_{d-1}-\frac{\eta}{\sqrt{(G_{j2,f1})_d}} \cdot (g_{j2,f1})_d \end{aligned} \qquad(26)$$

2.3.4 关于初始参数的设定

文献1中如此建议：
（1）$\eta$：没有具体的建议，用户根据经验指定即可，一般会取0.1，0.01，0.001。

（2）$V$：在区间$[0,1/\sqrt{k}]$间的随机值，均匀分布即可。

（3）$G$：设置为1，以避免$(G_{j1,f2})_d^{-\frac{1}{2}}$出现很大的值。

2.4 时间复杂度

2.4.1 计算时间复杂度

由于式(18)无法做类似于式（10）的简化，因此FFM的计算时间复杂度为$O(kn^2)$。

2.4.2 训练时间复杂度

由于训练时，需要先根据式（18）计算$\phi$，复杂度为$O(kn^2)$，计算得到$\phi$后，还需要按照式（22）计算1次，按照式（21）计算2k次，按照式（23）计算2k次，按照式（24）计算2k次，也就是说，总的训练时间复杂度为：

$$O(kn^2) + 1 + 2k + 2k + 2k = O(kn^2)$$

因此，训练时间复杂度为$O(kn^2)$。

2.5 计算速度优化

2.5.1 openMP

OpenMP提供的这种对于并行描述的高层抽象降低了并行编程的难度和复杂度，这样程序员可以把更多的精力投入到并行算法本身，而非其具体实现细节。对基于数据分集的多线程程序设计，OpenMP是一个很好的选择。同时，使用OpenMP也提供了更强的灵活性，可以较容易的适应不同的并行系统配置。线程粒度和负载平衡等是传统多线程程序设计中的难题，但在OpenMP中，OpenMP库从程序员手中接管了部分这两方面的工作。

openPM原生支持C/C++/Fortran，但java可以通过jomp等引入，未测试。

2.5.2 SSE3

SSE3 中13个新指令的主要目的是改进线程同步和特定应用程序领域，例如媒体和游戏。这些新增指令强化了处理器在浮点转换至整数、复杂算法、视频编码、SIMD浮点寄存器操作以及线程同步等五个方面的表现，最终达到提升多媒体和游戏性能的目的。Intel是从Prescott核心的Pentium 4开始支持SSE3指令集的，而AMD则是从2005年下半年Troy核心的Opteron开始才支持SSE3的。但是需要注意的是，AMD所支持的SSE3与Intel的SSE3并不完全相同，主要是删除了针对Intel超线程技术优化的部分指令。
SSE3指令采用128位的寄存器，可以同时操作4个单精度浮点数或者整数，因此非常类似于向量运算。这对于有大量向量计算的的FFM模型是有用的。
但事实上，计算$\phi$是几乎无用，而这是最耗时间的部分。

2.5.3 ParameterServer

https://www.zybuluo.com/Dounm/note/517675
Paraeter Server框架中，每个server都只负责分到的部分参数（server共同维持一个全局共享参数）。server节点可以和其他server节点通信，每个server负责自己分到的参数，server group共同维持所有参数的更新。server manage node负责维护一些元数据的一致性，例如各个节点的状态，参数的分配情况。

2.6模型优化

2.6.1 特征编码连续

如果特征的编码不连续，比如编码是有意义的，或者预留空间给之后的编码。如果直接使用最大编码值的作为参数数据尺寸，则会导致大量内存空间的浪费，因此有2种解决方案：
（1）使用hashmap，而非数组。
（2）将有意义的编码映射到一个连续的编码空间。
目前我们使用方式（1），理论上方式（2）的计算速度会更快。

2.6.2 一次项缺失的影响

正如上面式（18）所言，我们经常会忽略了一次项的影响，因此我们可以为每个样本加上一个辅助特征，这项特征的值恒为1，这相当于引入了一次项。

2.6.3 样本归一化

文献1还建议，将样本向量的长度归一化后，性能有少量的提升。

$$R[i]=\frac{1}{||X||}$$

2.6.4 特征归一化

某些特征（如购买个数）有可能很大，而一些类别参数则恒为1，这将导致不同特征最终对模型的影响相关很大，这很不合理。

五、DEEP & WIDE

赏